Interactive illustrated interplanetary guide and calculator for KSP
by olex, based on Kosmo-not's interplanetary how-to guide
Performing a transfer from an orbit of one body directly to an orbit of another one seems like serious business. A few guides published on the forums have a lot of maths and stuff, you may think this is too complicated to figure out.
Well, it is rocket science, but: it's not complicated.
What if I can demonstrate that to perform such a transfer, all you need to calculate are just two angles and your escape velocity? For all calculations, you only need to know the orbital parameters of the body you are flying from, the body you are headed to, and the orbit of your own ship.
Important: the information in this guide does not account for eccentricity or inclination of planetary orbits.
What do we need to know?
What are these two angles I am talking about? Let me show you:
-
The planetary phase angle is the angle your destination planet or moon needs to be in front or behind your origin along its orbit. You want to know this, so that you can actually meet up with the destination planet at the end of the transfer.
-
The ejection angle is the angle, at which you want to start your transfer burn in your origin planet's or moon's orbit. You want to get this angle right in order to escape the sphere of influence of your origin parallel to its own orbital prograde or retrograde heading.
The escape velocity is how fast your spacecraft will need to go in order to escape the origin body's sphere of influence and go onto the intercept trajectory to the target body. It can be expressed as the sum of you parking orbit velocity and Δv applied during the escape burn.
To calculate these three values, you can either:
- Check out the guide this page is based on, written by Kosmo-not on the KSP forum: click here .
- Or use the handy transfer calculator provided on the right.
How to use these values?
Using these values for interplanetary flight is no more complicated than obtaining them:
- Place your ship in a circular, 0° inclination parking orbit around your planet/moon of origin. For optimal efficiency, make this orbit at a 90° heading.
- Obtain the planetary phase angle, ejection angle and ejection velocity values according to your origin's orbit, your destination's orbit and your parking orbit information, as described above.
- Timewarp until the planetary alignment is right. For a positive phase angle, you want the destination to be ahead of you, and for a negative phase angle you want it behind you.
- Timewarp some more, until your ship is properly positioned for the transfer burn in the parking orbit. You need to put yourself at the ejection angle before your origin's prograde (for a higher destination orbit) or retrograde (for a lower destination) orbital heading, as shown in the right image.
- Once positioned, turn prograde and burn, until you reach ejection velocity.
Zoom out to see your orbit's intersection with the target planet's orbit. If the orbits don't match at the destination, perform minimal pro- or retrograde correction burns to achieve intercept. If you have your maximum conics set to 3 or more in settings.cfg, you will see the target body intercept once you get it right. Congratulations, you are on your way to another planet!
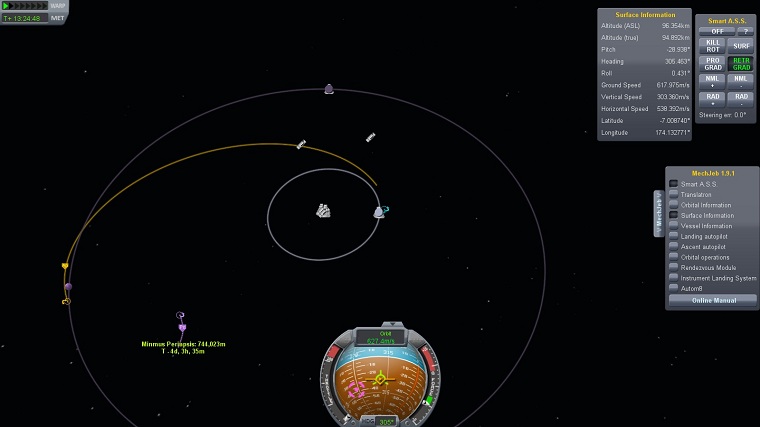
Once you have achieved an intercept trajectory, minimal pro- or retrograde burns (sometimes made with RCS translation, in order to not overdo them) can allow you to adjust the periapsis at your destination. Use this to put yourself into a direct atmospheric capture, or adjust it otherwise to your liking.
Conclusion
I hope you have found this guide and calculator to be useful!
I want to thank Kosmo-not for making his great guide available on the forums for me to base this on, maltesh for helping me out with some of the math, and Elembis for modifications to the code. Without these guys, this wouldn't exist.